Aplicaciones

 

APLICACIONES  EN LA COTIDIANEIDAD

Con la idea de comprobar los fenómenos presentes en la teoría de la relatividad especial, diversos científicos se dieron a la tarea de generar artefactos e instrumentos capaces de dar una visión materializada y aplicada en artefactos de uso común.

Un ejemplo concreto es el Sistema de Posicionamiento Global, también conocido como GPS, diseñado por el Departamento de Defensa de los Estados Unidos, el cual ofrece una posibilidad muy precisa de localizar  cualquier objeto o lugar sobre la tierra. Para determinar una aproximación exacta de la posición de un usuario u objeto, este sistema requiere de cuatro o más satélites en conjunto con una serie de cálculos matemáticos que posibilitan aproximarse al punto casi exacto del objeto o lugar. (GPS.Gov, sf).

Se desprenden de este tipo de tecnología aplicaciones mucho más elaboradas en la actualidad como Google Maps, Waze, e incluso Maps.me, ésta última aplicación tiene la gran ventaja de que no requiere de datos móviles, únicamente se descarga el mapa del lugar y funciona vía satélite en tiempo real.

Los relojes atómicos, fue otra aplicación diseñada con la intención de determinar y medir con precisión el tiempo, comprobar el fenómeno de la dilatación del tiempo, (que más adelante se detallará) y aportar a exploraciones realizadas para determinar el comportamiento de la materia oscura. ( ABC Ciencia, 2021).

Otras de las aplicaciones son los dispositivos láser, que en la actualidad tienen variedad de usos desde comercios, estéticas, salud entre otros, por ejemplo en las lecturas de códigos de barras,  punteros que se usan para realizar presentaciones, tratamientos estéticos para reducción de manchas que funcionan bajo la dinámica de este tipo de tecnología y cirugías específicas que demandan alta precisión. ( BBA, 2019).

Adicionalmente se podrían considerar otros aportes dado el gran entendimiento del espacio, tiempo y la forma en cómo se comporta la luz con la teoría de la relatividad. De esta forma, los aparatos que transforman la luz en electricidad como el caso de paneles solares, la precisión de las farolas o lámparas que de forma automática se cargan durante el día y encienden en la noche, esto a partir de la ley del efecto fotoeléctrico, el punto clave para estos aportes de Einstein, fue el visualizar que la luz no se distribuía de manera uniforme, alterando nuevamente los aportes clásicos de la época. 

Para Einstein la luz se concentraba en paquetes separados, estableció con esto los cálculos matemáticos desde los cuales logró encontrar que las partículas de luz (fotones) impactan en un material y movilizan sus electrones, al generarse esa colisión, los fotones ceden la energía impulsando esas partículas a otros átomos produciendo una corriente eléctrica. (Fundeen. 2021).

Finalmente, con los diferentes fenómenos producto de la teoría de la relatividad especial, ha sido posible que los científicos puedan predecir fenómenos cósmicos, un ejemplo de esto son los lentes gravitacionales o lupas cósmicas, para Einstein en puntos específicos del universo hay mayor concentración de masa, por ende hay más atracción gravitacional, lo que afecta a los rayos de luz que pasan cerca, esto hace que se desvíen simulando que pasan a través de lupas o lentes gravitacionales, con esa lógica, los cuerpos que están detrás de estas lentes se pueden percibir mejor desde la tierra y tener la posibilidad de ser estudiados.

Figura 1. Alma Kids, (sf).

Gracias a esos detalles, para el año 2015 fue posible observar la imagen de una supernova y así entender como se originan, ese fenómeno fue denominado cruz de Einstein. (Pérez, 2015). 

Aplicaciones de los fenómenos para entender su naturaleza

Respecto a la aplicación de ambos fenómenos, es necesario repasar algunas consideraciones claves que nos aportan autores como: Cervantes & Rodríguez (2006), Gómez (2007) y Tipler & Mosca (2021):

• La velocidad de la luz es absoluta y tiene un valor constante C: 299 792 458 (m/s). De acuerdo con Einstein, esta velocidad siempre será la misma respecto al observador, independientemente del movimiento de éste.
• El tiempo es relativo. No es un parámetro universal, es una dimensión que se puede recorrer, y es capaz de alterarse con el movimiento en el espacio.
• Entre más rápido nos movemos el tiempo transcurre más lento.
• El tiempo y el espacio no son absolutos como la luz, éstos se transforman con el movimiento.
• El tiempo y el espacio se comprimen de forma particular para una persona en movimiento.
• Para mantener una velocidad constante requiero moverme a una distancia y tiempo menor.

Simultaneidad de la relatividad

Para entender el fenómeno de la simultaneidad es preciso experimentar sucesos que ocurran al mismo tiempo, por ejemplo: si tenemos dos observadores A y B que están en un mismo sistema de referencia inercial, en ese momento para ellos la simultaneidad del evento es absoluta, pues se encuentran en reposo, sin embargo, no siempre puede que se perciba de esa forma, pues en otro momento si uno de estos observadores estuviese en movimiento,  los eventos no serán simultáneos si no que serán sucesos relativos. (Tipler & Mosca, 2021). Se puede observar el siguiente video de Ranfaeamon (2013a), que permite ampliar este fenómeno:

  : 

Adicionalmente, un ejemplo de aplicación de dicho fenómeno se evidencia cuando un observador que se llamará observador Raúl está a la mitad del camino entre dos puntos A y B, en los que se producen dos acontecimientos de forma simultánea; de forma sincronizada emiten dos destellos luminosos, como se aprecia en la figura 2.

                                       Figura 2. Ejemplo 1 de simultaneidad. Elaboración propia.

Los destellos que producen los puntos A y B, viajan como ondas luminosas en todas las direcciones, se producirá entonces un rayo de luz que viajará de A hasta Raúl y también de forma simultánea otro rayo de luz que viajará desde B hasta Raúl, llegando a un momento en el que ambos destellos de luz se entrecrucen y sean percibidos por Raúl al mismo tiempo, ya que la velocidad de la luz es constante, como se aprecia en la figura 3.

                                         Figura 3. Ejemplo 2 de simultaneidad. Elaboración propia.

 

Hasta aquí, se podría hablar de un fenómeno de simultaneidad que es absoluto, pues tanto A, B como el observador Raúl estaban en un mismo sistema de referencia inercial.

Pero, que pasaría si otro agente observador (observador prima) al que llamaremos Catalina se suma al experimento y está en movimiento,  con una velocidad determinada respecto al observador Raúl.

En este caso, lo que sucederá es que para Catalina los eventos no sucederán de la misma forma en cómo los percibió Raúl, según la velocidad que lleve Catalina en el momento puntual en el que Raúl perciba ambos destellos de luz a cómo se apreció en la figura 2, es posible que en ese instante Catalina esté más cerca del punto B y observe primero el destello de luz que emite B. Tómese en cuenta que la luz siempre se va a mover a una velocidad constante, ver representación en figura 4.

       Figura 4. Ejemplo 3 de simultaneidad. Elaboración propia.

 

Es aquí donde se dermina que el fenómeno de la simultaneidad no se puede percibir igual por todos los observadores, notemos que Catalina se mantuvo en movimiento a diferencia del observador Raúl, por tanto, Catalina no percibió igual que el observador Raúl la simultaneidad de los destellos de luz, ella observó primero el destello de luz que emitió B y luego el que emitió A, mientras que Raúl percibió ambos destellos al mismo tiempo.

 

 Dilatación temporal

En cuanto a la dilatación del tiempo, una de las primeras pruebas realizadas para comprobar dicho fenómeno fue mediante el experimento de los relojes atómicos de cesio, realizado por el físico John Haefely y el astrónomo Richard Keating en 1971.  El experimento consistía en sincronizar ambos relojes a la misma hora pero en dos escenarios diferentes, uno de ellos estaría estacionario en la tierra, sin moverse, mientras que el otro reloj estaría en los cielos volando alrededor del mundo, ver figura 5.

                                    Figura 5. Wikipedia, (2017). Experimento de Haefey y Keating

 De acuerdo con los planteamientos de Einstein lo que se quería comprobar era la existencia de la variación del tiempo entre ambos relojes. Considerando aspectos como la fuerza de gravedad,  la velocidad y  el estado de reposo del otro reloj que estaba estático,  se pudo evidenciar que el reloj que estaba dentro del avión estaba retrasado respecto al reloj estacionario en la tierra por 40 mil millones de segundo. Comprobando así una de las consideraciones anotadas al inicio “Entre más rápido nos movemos el tiempo transcurre más lento”.

En el siguiente video se explica en detalle el experimento de Haefely y Keating, en Ranfeamon, (2013b).

 

 

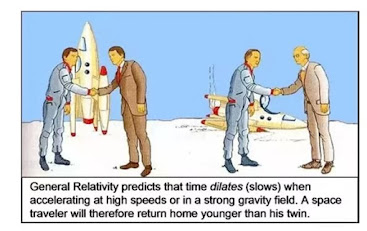
Otro ejemplo que probablemente sea más representativo a nivel visual, es la paradoja de los gemelos, entiendo por paradoja, de acuerdo con el diccionario de la Real Academia Española: “un hecho que es contrario a la lógica”. (RAE, 2021).

Con este ejemplo es posible notar la dilatación del tempo cuando se viaja a velocidades cercanas a la luz, de forma que uno de los gemelos ( Gemelo A) realiza este viaje espacial a una estrella cercana, (a unos cuantos años luz) mientras que el otro gemelo ( Gemelo B) se queda estático ( inerte) en la tierra. ¿Qué ocurre? ¿Cuál es la paradoja?

De acuerdo con la teoría de la relatividad lo que cambia es la percepción del marco de referencia, para el Gemelo A, es su hermano el que se mueve respecto de él, no percatándose que es el (Gemelo A) quién se distancia de la tierra debido a la gran velocidad con la que se mueve en el espacio, ya más adelante lo notaría al acelerar y desacelerar en su trayecto, de forma que su viaje, no está dentro de un marco de referencia inercial. Ver figura 6. 

 Figura 6. Vané, (sf). Dilatación del tiempo

Es así como para el Gemelo A, el tiempo transcurrirá más lento pues está en constante movimiento,  en comparación con el Gemelo B que se quedó estático en la tierra y la paradoja se hará presente cuando al regresar a la tierra el Gemelo A note que su hermano (Gemelo B) está mucho más envejecido que él. Se puede visualizar la explicación completa en el siguiente video de Ranfeamon, (2013c):

 

 En la aplicación de ejercicios prácticos, se contempla la siguiente ecuación ( ver figura 7),  que permite relacionar el tiempo transcurrido por un observador en estado de reposo respecto a otro en movimiento

  Figura 7. Veloso (2017).  Ecuación paradoja de los gemelos.

 

Para atender la primera pregunta se tienen los siguientes datos:

 Edad del papá: 50 años

Tiempo de duración en el espacio por parte de Laura: 10 años.

 

Al tener los datos anteriores, se puede estimar que al regreso de Laura, su papá tendrá 60 años.

Sin embargo,  para atender la segunda pregunta, es necesario hacer uso de la fórmula:

 

Donde se tiene que:   10 años es el equivalente a: 3.154 segundos.   C: 0.6 c.     Δt= _3.154 s      =      1-(0.6. c )2                 C2   Δt= _3.154 s    = 20183 s = 6.3 años.          1-0.6 2     Laura que al iniciar el viaje tenía 30 años, al momento de regresar a la tierra tendrá:  30 + 6.3= 36.3 años.